Угу. Я об этом писал выше. Почитай, что такое предел пропорциональности, после превышения которого деформации из упругой стадии переходят в пластическую. "Малые деформации" - это скорее от стержней пошло. Т.к. они не должны деформироваться в процессе работы. Поэтому если стержень сильно сжать или растянуть, он перестаёт выполнять свои задачи. С той же вики про пружины
Витые металлические пружины преобразуют деформацию сжатия/растяжения пружины в деформацию кручения материала из которого она изготовлена, и наоборот, деформацию кручения пружины в деформацию растяжения и изгиба металла, многократно усиливая коэффициент упругости за счёт увеличения длины проволоки противостоящей внешнему воздействию.
Там по сути деформации очень маленькие получаются. Когда мы растягиваем пружину, проволока, из которой сделана пружина немного вращается вокруг своей оси и практически не растягивается. Поэтому для пружин закон Гука вполне применим.
А в гитаре самая обычная среда. Там нет высоких температуры, давления.
Ты мне скажи, что такое идеальная сталь. Определение. Когда в физике применяют термин "идеальный", подразумевают какие-то характеристики, которые недостижимы в реальности. Но эти идеальные характеристики описаны довольно точно.
И я ещё раз повторю - ты знаешь, как рассчитывается коэффициент упругости? Посмотри. Там даже формула для цилиндрической витой пружины есть, которая учитывает "сложную геометрическую систему". И этот коэффициент для пружины будет линеен на всей стадии упругой деформации.
Пока ищешь ответы, расскажу.
Сталь делят на марки. И не просто так, а по значению различных характеристик. Для получения стали каждой марки применяются различные технологии. Каждую партии должны на производстве проверять в лаборатории на соответствие марки. Для каждой марки есть какой-то допустимый разброс характеристик. Если образец в лаборатории подходит по параметрам, значит всей партии присваивают марку. И вот когда инженер рассчитывает систему, он в ходе расчётов (сопромат в основном) получает характеристики, которые необходимы, чтобы система работала так, как положено, по сути не развалилась. Дальше он под эти характеристики подбирает марку стали. И когда он марку подбирает, в расчётах подразумевается, что сталь обладает именно теми характеристиками, которые заявлены в марке. По факту есть разброс, т.к. да, мир не идеален. Но этот разброс в пределах допустимых значений. Поэтому инженер, используя сталь определённой марки и указывая потом эту сталь в документации к проекту, может быть уверен, что конструкция будет работать как должна.
Плюс в большинстве инженерных расчётов закладываются коэффициенты надёжности. Просто значения умножаются, например, на 1.2. Коэффициент зависит от среды работы изделия и сооружения. Это всё прописано в государственных стандартах - где и сколько надёжности закладывать.
Поэтому идеальной стали не только в реальности не существует. Есть марки стали, которые обладают заявленными характеристиками. И если конструкция развалится, пострадают люди и экспертиза установит, что характеристики стали не соответствуют её марке, то тому, кто в лаборатории эту сталь не забраковал, а пустил на реализацию ,могут и уголовку впаять. Так что с этим всё серьёзно.
Вот посмотри, как марка описывается
http://metallicheckiy-portal.ru/marki_metallov/stk/20Как это относится к закону Гука?
А вот так. Посмотрим на формулы расчёта коэффициента жесткости.
Для стержня

Е — модуль Юнга, зависящий только от материала, из которого выполнен стержень;
S — площадь поперечного сечения;
L
0 — длина стержня.
Как видим, коэффициент зависит не только от геометрических характеристик, но и от стали. Ну или другого материала. Соответственно у нас в модуле юнга уже заложено, как сталь ведёт себя при деформации. Это сделано для упрощения расчётов. Если мы полностью развернём формулу закона Гука, то коэффициент жесткости превратится в формулу выше, модуль Юнга тоже хитро считается, и т.д. и т.п. Но так как у нас все материалы стандартизированы, не нужно каждый раз пересчитывать всё, можно воспользоваться готовыми модулями и коэффициентами.
Для пружины же формула расчёта коэффициента жесткости абсолютно другая
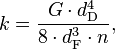
d
D — диаметр проволоки;
d
F — диаметр намотки (измеряемый от оси проволоки);
n — число витков;
G — модуль сдвига (для обычной стали G ≈ 80 ГПа, для меди ~ 45 ГПа).
Тут видно, что в формуле пропал модуль Юнга, который характеризует реакцию материала на растяжение/сжатие, зато появился модуль сдвига.
Ещё раз повторю, закон Гука работает в стадии упругой деформации. Он линеен и зависит от длины растяжения. Коэффициент - это постоянная. Это уже математика. Если нужен переменный коэффициент, то для формулы задаются границы, где меняется коэффициент. Иначе это уже не коэффициент, а переменная.
А линейность коэффициента зависит от того, как он введён в формулу. Если это просто множитель, как в законе Гука, это линейный коэффициент. Если коэффициент в формуле возводится в квадрат, это квадратичный коэффициент и т.п.
В общем закон Гука для пружины такой же как и для стержня. Разница в расчёте коэффициента жесткости.
... и добавил:По законам ньютона.
В физике есть статика - неподвижные системы, а есть динамика. Вот в статике. которую мы сейчас рассматриваем, второй закон не используется в чистом виде. Он используется только если нужно расписать участвующие силы
Наиболее просто условия статики формулируются в евклидовой системе координат. В число законов статики входят в основном первый и третий законы Ньютона. Они присутствуют в том виде, в котором равнодействующая сила в каждой точке равна нулю, или что эти силы контактные и приложены вдоль одной и той же линии и уравновешивают друг друга. Второй закон Ньютона в своем исходном виде не применяется, а применяется в форме расшифровки приложенных к м.о. сил, например, сил упругости, трения и притяжения к земле.
... и добавил:И да, когда считаются сложные системы, их отдельно рассчитывают на статические и динамические нагрузки.