DSP DIYУрок 1Попробую начать некоторую инициативу по ознакомлению общественности с изнанкой аудио-технологии, в качестве старта возьму такой вопрос как подгонка АЧХ сигналов, точнее получение подгоночных импульсов. Естественно в данном случае будет рассматриваться далеко не распространенные средства для этого, такие как iZotope Ozon и Voxengo Curve EQ с последющей деконволюции, а нечто совсем другого уровня точности.
Особо пытливые умы могут попытаться это повторить, для этого “всего лишь” потребуется Matlab, где это взять я думаю многие и так знают

Правда для одноразового опыта я бы порекомендовал найти portable-версию, чтобы не маяться с установкой лицензии.
Почему именно Matlab, когда я изначально реализовал такой подход в Wolfram Mathematica? Ответ прост – у него есть встроенные функции для подобного, в то время как в математике многое пришлось писать самому на основе более базовых вещей.
Tone matching MATLABНа самом деле бояться ничего не нужно, достаточно выполнить несколько команд с модификацией под собственные данные.
В данном случае я использую исходные готовые файлы на своём жёстком диске.
1. Для начала, нам надо загрузить необходимые аудио-данные, в Matlab это можно сделать либо командами, либо воспользовавшись импортом данных из меню.
[target,fs]=wavread('H:\Backup\Audio\Clang test\Fortin.wav','double');
source=wavread('H:\Backup\Audio\Clang test\CCS_RG75R.wav','double');
target это данные для того что мы бы хотели получить,
source это источник, если использовать функцию импорта, то лучше сразу обозвать переменные так же, чтобы не менять в дальнейшем. Формат немного меняется, так как в первом случае попутно получается частота сэмплирования файла, во втором случае это опущено, полагается что частоты сэмплирования совпадают.
2. Далее определим размер блока, для разрешения лучше 1 Гц, размер блока должен превышать частоту сэмплирования и являться степенью двойки.
nfft=2^nextpow2(fs);3. Рассчитаем окно, я взял окно Кайзера, т.к. для этого есть готовая функция, в математике же я предпочёл использовать окно KBD (Kaiser-Bessel Derived), всё равно писать с нуля надо было

w=kaiser(nfft,8);4. Теперь настал черёд определения осреднённых спектров сигнала, для этого в Matlab имеется готовая функция pwelch() (анализ Велча).
target_spectrum=pwelch(target,w,nfft/2,[],[],'twosided');
source_spectrum=pwelch(source,w,nfft/2,[],[],'twosided');
В-принципе, пункт 3 можно было опустить и воспользоваться окном по умолчанию, тогда вместо w в вызове функции следовало бы указать размер окна, nfft.
5. Вот теперь можно поделить один спектр на другой и получить подгоночный:
matching_spectrum=sqrt(target_spectrum./source_spectrum);
Так как pwelch() даёт осреднённый спектр возведённый в квадрат, то необходимо взять корень, я предпочёл это сделать один раз.
6. Вот тут возможны два подхода, рассмотрим каждый.
Для получения импульса надо просто выполнить обратное преобразование Фурье для спектра.
imp=ifft(matching_spectrum);
Но давайте взглянем, что из себя представляет этот импульс?
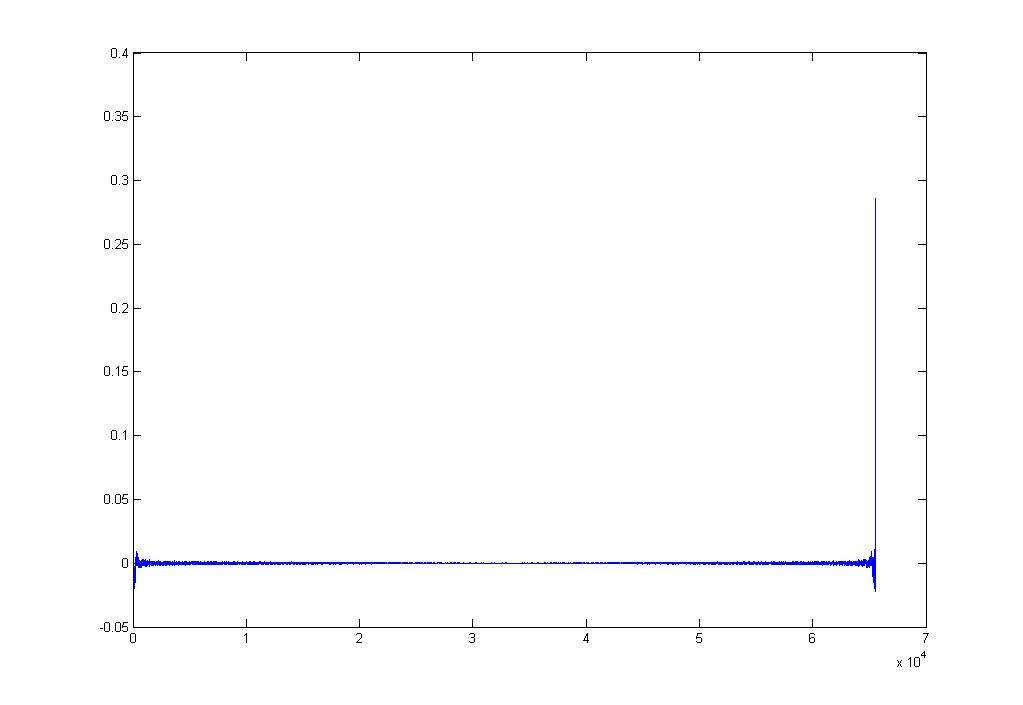
Видно что импульс имеет пики в начале и в конце, если загрузить его в таком виде в импульсник, то будет слышно эхо. Если выкинуть его половину, то частотка поменяется, если взять вторую половину перед первой, то частотка не изменится, эха не будет, но будет большая задержка и преэхо. Это стандартно для фильтров с линейной фазой.
Что делать?
И вот тут нам на помощь приходит так называемое преобразование импульса к минимальной фазе. Есть различные способы это сделать, но изящнее всего воспользоваться гомоморфной фильтрацией (Homomorphic filtering, классный термин, не так ли?) или кепстральной обработкой (от CEPStrum, фактически SPECtrum наоборот).
Но не стоит выпадать в осадок, Матлаб имеет встроенную функцию для этого, так что ничего особо делать не надо.
[y,mpimp]=rceps(imp);
Давайте взглянем на получившийся импульс mpimp:
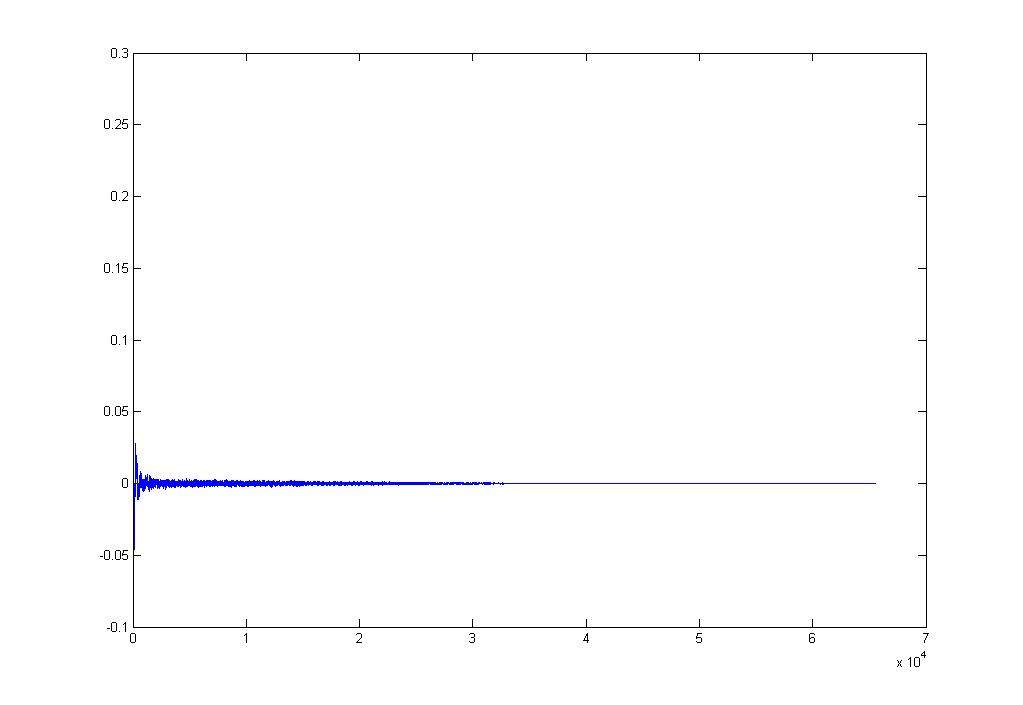
Совсем другая картина, не так ли?
Причём частотка в данном случае не меняется.
7. Остаётся нормализировать импульс и сохранить в wav.
mpimp=mpimp/max(abs(mpimp));
wavwrite(mpimp,fs,32,'H:\Backup\Audio\Clang test\CCS_RG75R_to_Fortin_imp_matlab.wav');
А теперь вспомним что в 6 я говорил про два варианта.
Второй вариант просто состоит в том чтобы не получать обычный импульс, а сразу произвести кепстральную обработку спектра самим, тем самым избежав дополнительных обратного и прямого преобразований Фурье.
cepstrum=ifft(log(abs(matching_spectrum)));(это и был пресловутый кепстр)
hmfilter=[1;2*ones(nfft/2-1,1);ones(1-rem(nfft,2),1);zeros(nfft/2-1,1)];(а вот это был гомоморфный фильтр)
mpimp=real(ifft(exp(fft(hmfilter.*cepstrum))));И далее по пункту 7.
Естественно названия файлов и путь у вас будут свои.
Для чего ещё это можно использовать?
А можно это всё использовать, помимо подгонки, для деконволюции сигналов.
В этом случае в качестве source выступает синусоидальный свип (синус с меняющейся частотой), а в качестве target записанный через мощник-каб-мик сигнал.
Дополнительно прикреплю полный код, которы можно вставить в M-file матлаба (File->New->M-file) и выполнить в один приём (естественно пути к файлам заменяем на свои).
[target,fs]=wavread('H:\Backup\Audio\Clang test\Fortin.wav','double');
source=wavread('H:\Backup\Audio\Clang test\CCS_RG75R.wav','double');
nfft=2^nextpow2(fs);
w=kaiser(nfft,8);
target_spectrum=pwelch(target,w,nfft/2,[],[],'twosided');
source_spectrum=pwelch(source,w,nfft/2,[],[],'twosided');
matching_spectrum=sqrt(target_spectrum./source_spectrum);
imp=ifft(matching_spectrum);
[y,mpimp]=rceps(imp);
mpimp=mpimp/max(abs(mpimp));
wavwrite(mpimp,fs,32,'H:\Backup\Audio\Clang test\CCS_RG75R_to_Fortin_imp_matlab.wav');
ps. Конечный импульс можно обрезать по вкусу, я обычно в вейвлабе обрезаю до 200 мс и в конце фейдаут применяю небольшой.
ps.ps. Для желающих самим проводить эксперименты, рекомендую вариант с бесплатным пакетом
SciLabhttps://guitarplayer.ru/index.php?topic=266917.msg6143050#msg6143050ps.ps.ps Более простой инструмент для создания подгоночных импульсов, реализующий данную методику в рамках одного маленького приложения:
https://guitarplayer.ru/index.php?topic=319541.0